新手教程-最大割问题¶

问题描述¶

最大割问题是NP完备问题. 给定一张图, 求一种分割方法, 将所有顶点分割成两群, 同时使得被切断的边的数量最大,或边的权重最大.

以无向无权图为例. 在图 \(G(V,E)\)中, \(V\)为图的顶点集合, \(E\)为图的边集, \(w\)为图的邻接矩阵. 对于 \(i,j∈V\), \(w_{ij}\)表示顶点 \(i\)到顶点 \(j\)是否有边, 有连边关系则取 \(1\),无连边关系则取 \(0\). 以决策变量 \(\sigma_i\)表示顶点 \(i\)的分类, 其可能的取值为 \({1,-1}\),分别表示将顶点 \(i\)分为A类或B类.

则在给定的无向图中，将所有顶点分割成两群的分割方法所对应割取的边的个数为Z，模型表示为:

\[max Z = (\sum_{i<j,i∈V}\sum_{j∈V}w_{ij}-\sum_{i<j,i∈V}\sum_{j∈V}w_{ij}\sigma_i\sigma_j)/2\]

以一个四顶点实例说明，如下图所示，通过观察可以发现将1、2分为A类，3、4分为B类的“割”法将得到问题的最优解 \(Z=4\).

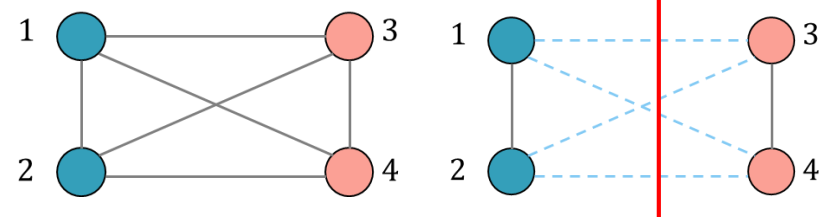
通过连边关系可知，邻接矩阵为

\[\sum_{i<j,i∈V}\sum_{j∈V}w_{ij} = w_{12}+w_{13}+w_{14}+w_{23}+w_{24}+w_{34}\]

\[\sum_{i<j,i∈V}\sum_{j∈V}w_{ij}\sigma_i\sigma_j = w_{12}\sigma_1\sigma_2+w_{13}\sigma_1\sigma_3+w_{14}\sigma_1\sigma_4+w_{23}\sigma_2\sigma_3+w_{24}\sigma_2\sigma_4+w_{34}\sigma_3\sigma_4\]

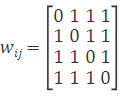
当顶点1、2为一组，顶点3、4为另一组时, \(\sigma_1=\sigma_2=1, \sigma_3=\sigma_4=-1\). 则上式变为

\[\sum_{i<j,i∈V}\sum_{j∈V}w_{ij}\sigma_i\sigma_j = w_{12}-w_{13}-w_{14}-w_{23}-w_{24}+w_{34}\]

此时目标函数为

\[max Z = (\sum_{i<j,i∈V}\sum_{j∈V}w_{ij}-\sum_{i<j,i∈V}\sum_{j∈V}w_{ij}\sigma_i\sigma_j)/2= w_{13}+w_{14}+w_{23}+w_{24} = 4\]

最大割数量为4，符合前文通过观察得到的答案。

注意到, \(w_{ij}\)为输入的常量，并不影响模型的计算，所以上式可以简化为：

\[min H = \sum_{i<j,i∈V}\sum_{j∈V}w_{ij}\sigma_i\sigma_j\]

其中, \(H\)表示哈密尔顿量, \(w\)为输入的邻接矩阵,决策变量 \(\sigma_i\)表示顶点 \(i\)的分类,上述式子就是一个最大割问题的Ising模型.

建模代码¶

输入矩阵¶

import numpy as np
import kaiwu as kw

# Import the plotting library
import matplotlib.pyplot as plt

# invert input graph matrix
matrix = -np.array([
                [0, 1, 0, 1, 1, 0, 0, 1, 1, 0],
                [1, 0, 1, 0, 0, 1, 1, 1, 0, 0],
                [0, 1, 0, 1, 1, 0, 0, 0, 1, 0],
                [1, 0, 1, 0, 0, 1, 1, 0 ,1, 0],
                [1, 0, 1, 0, 0, 1, 0, 1, 0, 1],
                [0, 1, 0, 1, 1, 0, 0, 0, 1, 1],
                [0, 1, 0, 1, 0, 0, 0, 0, 0, 1],
                [1, 1, 0, 0, 1, 0, 0, 0, 1, 0],
                [1, 0, 1, 1, 0, 1, 0, 1, 0, 1],
                [0, 0, 0, 0, 1, 1, 1, 0, 1, 0]])

使用CIM模拟器查看量子比特演化¶

查看单次CIM模拟的量子比特演化过程用到了kaiwu.cim.simulator_core模拟器, 该模拟器输入CIM-Ising矩阵、pump功率、噪声强度、圈数、圈步长, 输出量子比特演化的模拟量, 需要注意的是, 使用这个模拟器前一般会使用kaiwu.cim.normalizer对输入矩阵的特征值进行归一化:

matrix_n = kw.cim.normalizer(matrix, normalization=0.5)
output = kw.cim.simulator_core(
            matrix_n,
            c = 0,
            pump = 0.7,
            noise = 0.01,
            laps = 1000,
            dt = 0.1)

计算哈密顿量, 一般使用未进行归一化的矩阵进行计算:

h = kw.sampler.hamiltonian(matrix, output)

绘制量子比特演化图与哈密顿量图：

plt.figure(figsize=(10, 10))

# pulsing diagram
plt.subplot(211)
plt.plot(output, linewidth=1)
plt.title("Pulse Phase")
plt.ylabel("Phase")
plt.xlabel("T")

# Energy diagram
plt.subplot(212)
plt.plot(h, linewidth=1)
plt.title("Hamiltonian")
plt.ylabel("H")
plt.xlabel("T")

plt.show()

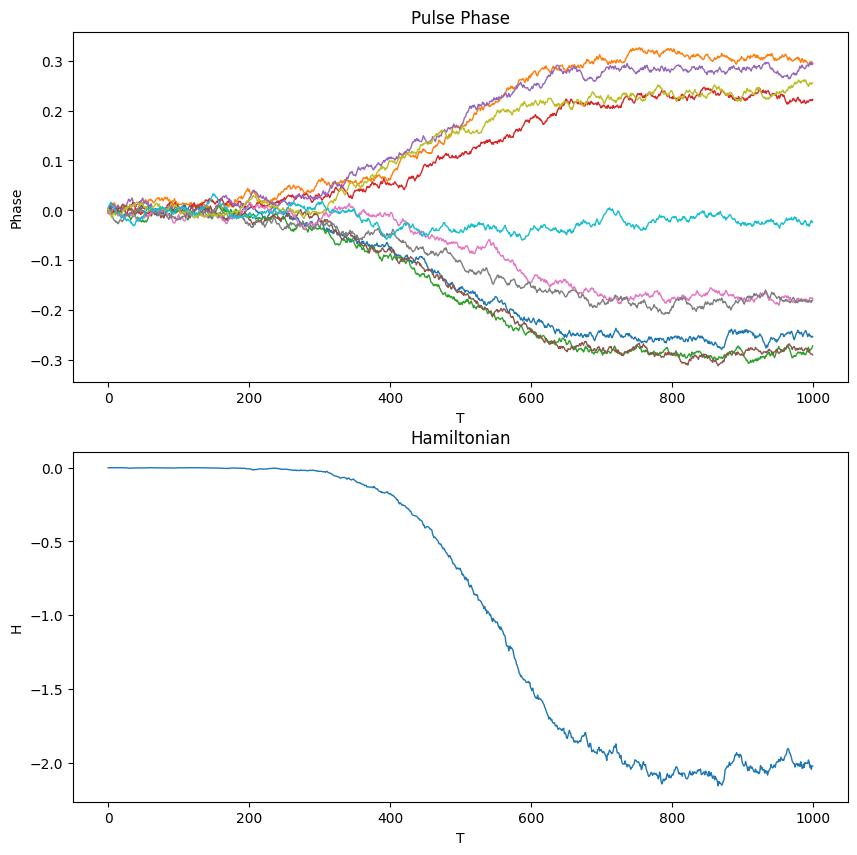
查看最优解查看最优解前需要将kaiwu.cim.simulator_core模拟器输出的数据使用kaiwu.sampler.binarizer进行二值化. 关于kaiwu.sampler.binarizer我们在本示例中只输入第一个参数表示输入解集, 其余参数保持默认即可.

c_set = kw.sampler.binarizer(output)

最优解采样, kaiwu.sampler.optimal_sampler将对二值的解集进行按能量排序, 越靠前的解能量越低, 即解越优.

opt = kw.sampler.optimal_sampler(matrix, c_set, 0)

取最优解, 其中 opt = (解集, 能量), 下面第一个索引取解集, 第二个索引取解集第一个解.

best = opt[0][0]
print(best)

模拟计算¶

使用CIM模拟器进行计算¶

若像大规模计算, 我们用到了kaiwu.cim.simulator模拟器, 该模拟器输入CIM-Ising矩阵、pump功率、噪声强度、圈数、圈步长、归一化因子、独立运行次数, 输出量子比特经过去重的二值化值, 使用这个模拟器前就不需要使用kaiwu.cim.normalizer对输入矩阵的特征值进行归一化了:

output = kw.cim.simulator(
            matrix,
            pump = 0.7,
            noise = 0.01,
            laps = 50,
            dt = 0.1,
            normalization = 0.3,
            iterations = 10)

输出结果¶

opt = kw.sampler.optimal_sampler(matrix, output, 0)
best = opt[0][0]
max_cut = (np.sum(-matrix)-np.dot(-matrix,best).dot(best))/4
print("The obtained max cut is "+str(max_cut)+".")