案例解析-任务调度问题（附量子计算对比）#

../../_images/jsp1.jpg

🙋‍♀️🙋‍♂️什么是任务调度问题（JSP）#

任务调度，这个听起来有点高大上的领域，其实在我们的日常生活中无处不在。你可以把它想象成是一位超级高效的秘书，负责安排公司里的各项工作任务。这位秘书要确保每个任务都能在合适的时间得到处理，既不能让员工闲着，也不能让工作堆积如山。在计算机科学中，任务调度就是这么一个角色，它负责**指挥计算机系统中的各种任务按部就班地进行**。

想象一下，我们的电脑或者手机，每天都要处理成千上万的任务，比如打开应用、运行程序、处理数据等。如果没有一个合理的调度策略，这些任务可能会相互打架，导致系统崩溃或者运行缓慢。任务调度的作用，就是像交通警察一样，指挥这些任务有条不紊地进行。它通过一系列精心设计的算法，比如优先级调度、轮询调度、公平调度等，来确保每个任务都能在适当的时候得到处理。

接地气一点来说，任务调度就像是我们厨房里的厨师长。你瞧，厨房里有洗菜的、切菜的、炒菜的，每个环节都有不同的任务。厨师长要根据客人的点单、食材的准备情况以及厨师的擅长领域，来合理安排每个人的工作。任务调度也是这样，它要根据任务的紧急程度、资源占用情况以及系统的整体负载，来决定哪个任务先执行，哪个任务后执行。

在逻辑严谨性上，任务调度领域的研究者们需要考虑的因素非常多。比如，如何保证重要任务优先执行，同时又不至于让不那么重要的任务饿死（即长时间得不到执行）；如何在多任务并发的情况下，合理分配CPU、内存等资源，提高系统的吞吐量；以及如何在任务执行过程中，动态调整调度策略，以应对不断变化的系统环境。

总之，任务调度是计算机科学中的一个关键领域，它不仅关系到我们日常使用的电子设备的性能，还涉及到数据中心、云计算、物联网等多个领域的效率和安全。通过对任务调度的深入研究，我们能更好地利用计算机资源，提高工作效率，让我们的生活和工作更加便捷。

应用案例：云计算中的任务调度🖧#

在云计算环境中，资源调度问题可视为一个JSP问题。具体来说，可以将云计算中的任务视为任务，服务器视为机器，通过调度算法优化资源利用率和任务完成时间。以下是一个基本的云计算任务调度示例：

  • 任务描述：客户提交一组渲染任务，每个任务有特定的计算量。

  • 目标：最小化所有任务的最大完成时间。

  • 解决方案：通过将任务分配给合适的服务器，使用量子计算技术优化调度方案，达到资源高效利用和任务尽早完成的目标。

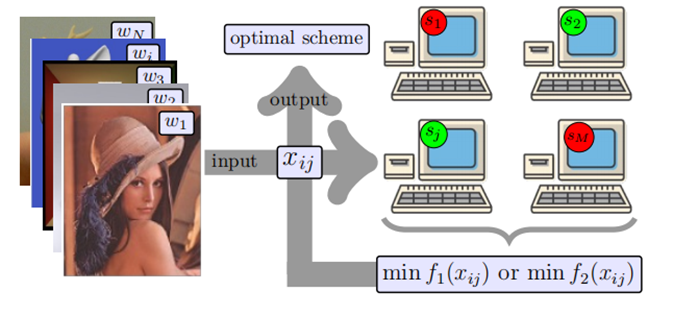
../../_images/jsp2.png

JSP 的基本组成包括：

  • 任务（Job）：需要完成的任务，每个任务只有一道工序。

  • 机器（Machine）：执行任务的资源，每台机器一次只能处理一个任务。

  • 调度（Schedule）：安排任务给不同的机器，并决策任务在机器上的执行顺序(事实上在本文中的JSP问题中，任务在机器上的执行顺序对结果无影响)。

为了将问题抽象简化，将多机任务调度问题的假设总结如下：

  1. 各任务需要的处理时间是一个确定的常数，只与任务有关；

  2. 各任务需要的处理时间与所在的机器无关，即假设各机器的任务处理效率一致；

  3. 各机器可以有不同的空闲开始时间，在此之前机器无法处理任务；

  4. 同一个任务只能被分配到一台机器上运行；

  5. 一台机器同一时刻最多只能处理一个任务；

  6. 机器在处理完一个任务后立即执行下一个被分配的任务直到完成所有被分配的任务；

  7. 所有的任务都要完成处理；

问题定义📖#

各个任务所需的运行时间以及各机器空闲开始时间取值为整数（比如取定义的时间精度的整数倍）。这样做便于将组合优化模型转为QUBO（Quadratic Unconstrained Binary Optimization，二次无约束二值优化）形式，以适配专用量子计算机。

为了规范化表述，将多机任务调度问题用到的集合与数据做以下定义：

定义机器集合 M，比如 M={机器1，机器2，…}，机器的数量表示为 |M|。

定义任务集合 N，比如 N={任务1，任务2，...}，任务的数量表示为 |N|。

定义任务 i \in V所需的处理时间为 w_{i}。

定义机器 j \in M的空闲开始时间为 S_{j}。

下面的示意图以4台机器处理10个任务为例，纵轴为机器，横轴为时间，每台服务器的空闲开始时间分别为1,2,3,4，后面每个带有数字的方块代表分配到各机器上的任务对应的时长，一个让整体完成时间最短的分配方案如图，该方案也是让各机器负载均衡的一个最优解，即各机器完成时间尽可能接近。

../../_images/jsp3.png

JSP 的数学描述及QUBO模型#

定义二值变量Xij，代表任务i是否分配到机器j上，如果任务i被分配到机器j，Xij=1，否则Xij=0。根据前述定义与假设，机器j的任务完成时间可表示为

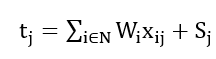
../../_images/jsp4.png

下面根据不同的目标，分别给出对应的QUBO模型。

🕐模型一最小化整体完成时间

针对第一种目标，即整体完成时间最短，首先建立组合优化模型如下：

定义变量为整体最晚完成的时间，也就是各个机器完成时间中的最大值，

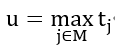
../../_images/jsp5.png

目标函数

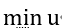
../../_images/jsp6.png

约束条件

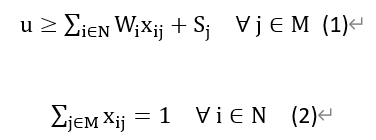
../../_images/jsp7.png

约束(1)表示最晚完成时间u不小于任何机器的完成时间tj，由于目标函数是最小化最晚完成时间u，变量u将取到满足(1)的最小值，也就是最晚完成的机器对应的完成时间。约束(2)限制了对于任何任务只能被一台机器执行。

为了适配量子计算，需要将上面的组合优化模型转为QUBO形式，QUBO特点是所有决策变量为二值变量，目标是二次函数，且无约束条件。由于目标为整数，可用基于多个二值变量的二进制来表示：

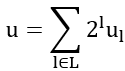
../../_images/jsp8.png

其中为二值变量，取值0或1。为需要的二进制位数集合，取决于数据的值。这样求解的最小值就转变为求解的取值。

下一步将不等式约束(1)通过增加松弛变量的方式转化为等式约束。所有的松弛变量都是非负的。约束(1)可表示为：

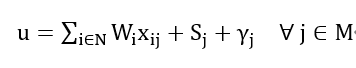
../../_images/jsp9.png

由于松弛变量也是整数，将其二进制化，约束(1)可进一步表示为：

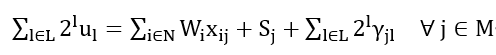
../../_images/jsp10.png

为了将等式约束化为目标函数的一部分从而满足QUBO形式，将等式约束改写为 f(x, u) = 0 的形式，然后将左侧取平方，乘以足够大的惩罚系数 \lambda 加入目标函数即可。这样当约束被满足，目标项中的相关项也就为0。目标最小化求解会倾向于让所有惩罚项为零，即所有约束被满足。这样，原模型就可以转化为以下QUBO模型：

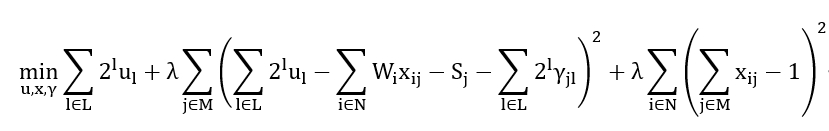
../../_images/jsp11.png

🕐模型二最小化各机器完成时间差距（负载均衡）

针对第二种目标，即各机器完成时间差异最小，将最小化各机器完成时间的方差作为优化目标，建立组合优化模型如下：

目标函数

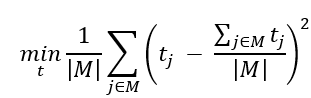
../../_images/jsp12.png

注意到各机器的平均完成时间与分配方案无关，是常数，将其定义为 \overline{C}。

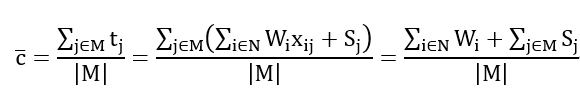
../../_images/jsp13.png

QUBO化的思路与上一模型一致，则QUBO模型可表达为：

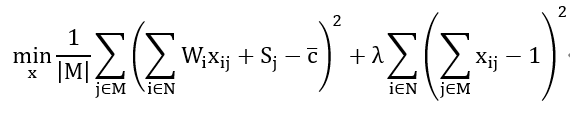
../../_images/jsp14.png

模型代码#

该代码可在Kaiwu SDK上运行求解。

import math
import numpy as np
import kaiwu as kw

# Output the number of unsatisfied constraints
def get_count_constr_not_met(solution_dict, print_detail=False):
    count_constr_not_met = 0  # Total number of unsatisfied constraints
    for t in SET_TASK:
        constr_value = kw.qubo.get_val(sum(x[(t, m)] for m in SET_MACHINE) - 1, solution_dict)
        if print_detail:
            print('constr_server_capacity', t, constr_value)
        if constr_value != 0:
            count_constr_not_met += 1
    return count_constr_not_met


# Output results
def result_summary(the_sol_dict):
    # Completion time for each machine
    max_complete_time = 0.0
    for m in SET_MACHINE:
        complete_time = kw.qubo.get_val(machine_endtime[m], the_sol_dict)
        if complete_time > max_complete_time:
            max_complete_time = complete_time
    return max_complete_time


if __name__ == '__main__':
    # Number of tasks
    N_TASK = 20
    # Number of machines
    N_MACHINE = 3

    seed = 12345
    np.random.seed(seed)

    # Index sets
    SET_TASK = {t for t in range(1, N_TASK + 1)}  # Tasks 1, 2, ..., N_TASK
    SET_MACHINE = {m for m in range(1, N_MACHINE + 1)}  # Machines 1, 2, ..., N_MACHINE

    # Model data
    DURATION = {t: np.random.randint(1, N_TASK + 1) for t in SET_TASK}  # Random task duration between 1 and 20
    START = {m: np.random.randint(1, N_MACHINE + 1) for m in SET_MACHINE}  # Random machine idle start time between 1 and 5

    # Penalty coefficient for constraints
    LAMBDA = 1000

    # Decision variables
    x = {(t, m): kw.qubo.Binary('x[' + str(t - 1) + '][' + str(m - 1) + ']') for t in SET_TASK for m in
         SET_MACHINE}  # Whether task i is assigned to machine j
    # QUBO objective function
    obj_function = 0.0
    # Variance term
    obj_function += sum(
        pow(
            START[m] + sum(DURATION[t] * x[(t, m)] for t in SET_TASK) -
            (sum(START[m] for m in SET_MACHINE) + sum(DURATION[t] for t in SET_TASK)) / N_MACHINE,
            2
        )
        for m in SET_MACHINE
    ) / N_MACHINE
    # Constraint term
    obj_function += LAMBDA * sum(pow(sum(x[(t, m)] for m in SET_MACHINE) - 1, 2) for t in SET_TASK)
    # End time for each machine
    machine_endtime = {
        m: START[m] + sum(DURATION[t] * x[(t, m)] for t in SET_TASK)
        for m in SET_MACHINE
    }

    qubo_model = kw.qubo.QuboModel()
    qubo_model.set_objective(obj_function)

    # Solve using simulated annealing
    max_iter = 40
    curr_iter = 0
    current_best = math.inf  # Initialize current best solution as infinity
    opt_obj = 0  # Desired optimal objective value (adjustable for specific problems)

    while (curr_iter < max_iter and current_best > opt_obj):
        print(f'Iteration {curr_iter} starts, current best solution = {current_best}')
        worker = kw.classical.SimulatedAnnealingOptimizer(
            initial_temperature=1000,
            alpha=0.99,
            cutoff_temperature=0.0001,
            iterations_per_t=10)
        solver = kw.solver.SimpleSolver(worker)
        # Get the optimal solution from simulated annealing output
        sol_dict, qubo_val = solver.solve_qubo(qubo_model)

        count_constr_not_met = get_count_constr_not_met(sol_dict, print_detail=False)
        if not count_constr_not_met:
            val_obj = result_summary(sol_dict)
            current_best = min(current_best, val_obj)  # Update current best solution

        curr_iter += 1
    print('Optimal solution:', current_best)

❇️总结#

任务调度问题（JSP）是一个复杂但实用的优化问题，广泛应用于制造业、项目管理和云计算等领域。尽管求解 JSP 具有挑战性，但通过使用各种先进算法和技术，例如量子计算，可以有效优化调度方案，提升系统效率和资源利用率。